今回は、グッドールの5大発明のなかの「平均律」である。もっとも、平均律よりは、そこに至る無数ともいえる音楽家たちの苦闘が主題ともいえる。
最初から余談になってしまうが、確かニュートンが、宇宙のことを理解するようになればなるほど、この宇宙は神が創造したものだという畏敬の念が強くなる、神の存在を意識せざるをえなくなる、と言っていた。しかし、音律の問題を考えると、とても神など存在するはずがないという意識になる。もし神が存在するとしたら、全知全能などとはほど遠い無能な存在か、あるいは能力があるのだとしたら、相当にいじの悪い存在だと思う。
さて、音楽が民族文化の相違を超えて、同質性がかなりの程度あるのは、音が自然現象だからだということを前に述べた。この音律の問題こそ、自然現象であることの特質が出てくる。そして、音律の実践的・理論的発展があったのは、ヨーロッパだけであるが、理論に限っていえば、かなり広い世界で同じことが論じられていたのだそうだ。いろいろな書物に、これから紹介することと、ほとんど同じことが、中国の古い文献に既に出てくるそうである。では、何故、音律はクラシック音楽の専売特許のようになったのか、それを今回考えてみよう。
ピタゴラス音階
ピアノの白鍵と黒鍵は、12の音からなっているが、この12の音はどのようにできてきたのかというのが、今回の主題である。第一回で紹介したように、音階が最初に定義されたのは、倍音の原理からであるとされる。しかし、倍音列は、上にいくほど、現在の１２音とはずれていくので、この倍音列で生じた音を並べて、１２音階ができたわけではない。
１２音階を最初に理論的な根拠をもって並べて見せたのが、有名なピタゴラスであることは、よく知られている。
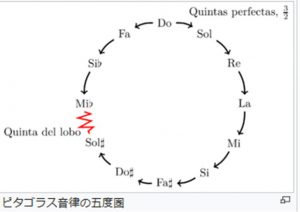
ピタゴラスは、数学者であるから、音を数学的に考察したわけだが、ふたつの音を重ねたときに、周波数が１対２であるときに、もっともよく協和することがわかった。もちろん、周波数を直接計測したわけではなく、絃を張って、絃を弾いたり、叩いたりすると音がでるが、長さを１対２にすることになって、協和音程を見つけたわけである。次によく協和するのは、長さが２対３のときであることがわかった。今風にいえば、基音と５度上のふたつの音である。そして、次々と５度上の音をとっていく。もちろん、あまり高くなると困るので、適当なところで、１対２の関係を利用して、つまり、オクターブさげて、音を決めていく。すると順番に次のようになる。
C → G → D → A → E → H → F♯ → C♯ → G♯ → D♯ → A♯(B) → E♯(F) → H♯(C)
という円環をつくって、Cにもどってくるから、１２種類の音ができるわけである。もし、ここで、最初のCとH♯としてのCとが同じ音、あるいは、正確にオクターブ上の音であるならば、神の存在を思わせたかもしれないが、実は、上のCは、オクターブ上、つまり、周波数が倍である音よりも、少し高くなってしまうのである。これは、自分で計算しても簡単にわかる。基音の周波数を決めて、(たとえば100)次々に1.5をかけていけばよい。数値が多くなったら、その都度、周波数を半分にすればよい。1.5という数値をずっとかけていくわけだから、かならずどこかで端数がでてきて、オクターブの上の音の周波数が200になるはずがないことは、だれでもわかるだろう。しかし、最初の出発の音とオクターブ上の音が、1対2にならないことは、最初の出発点が成立しないことになる。オクターブは最も協和するのでなければならない。だから、オクターブの1対2を確保すると、そのほかで調節しなければならなくなる。それをピタゴラスは、基音から5度ずつ下がる形で音列をつくり、シャープやフラットがたくさんつく音のところで調節することにした。
ラ♭とソ♯は、ピアノの鍵盤では同じ音だが、ピタゴラスの円環では異なる音である。しかし、これを同じ音として処理することで、１２音を確定したのである。
もちろん、そこのところは不自然になるが、しかし、音楽そのものが極めて単純で、歌は単旋律で、無伴奏であれば、全く問題ない。しかし、楽譜が発明され、複雑な音楽を作曲して、それを演奏することが可能になってくると、当然、音と音の重なりが出てきて、そこに協和しない音がたくさん出てくる。ピタゴラス音律は、オクターブ以外は、5度と4度だけが協和する。そこで、様々な「協和」のあり方に対応した音律が求められていくことになる。
現在でも重視されている純正律である。これは、基音と協和するように、12の音の高さを決めたものである。だから、一定の調性で演奏していれば、ふたつの音が濁ることが少なく、また、三和音が美しいハーモニーになる。しかし、純正律はあくまでもひとつの調性で完結するもので、異なる調に転調すると、協和関係は崩れてしまう。
純正律
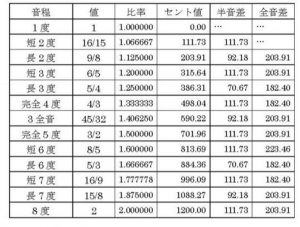上の純正律の音程の数値で見てみよう。
これをハ長調だとしよう。
1度と完全5度は3/2の関係となっている。ニ長調に転調するが、このままの数値を使うと、長2度と長6度が完全5度の関係になる必要がある。5/3を9/8で割ると、40/27となり、3/2でない。少数になおすと1.4848・・・・となる。1.5には近いが、完全5度になっていない。完全5度の音程にするためには、9/8に3/2をかける必要があり、27/16となり、表の5/3とは異なる値になる。つまり、ラの音がふたつあり、鍵盤を分けなければならない。24の調性ですべて純正律を貫徹するためには、どれだけたくさんの鍵盤が必要になるかわかるだろう。実際にそうのような楽器をつくったこともあるようだし、また近い音は無理にひとつで済ますとしても、数十の鍵盤が必要となる。それは、到底実用にはならない。弦楽器は響きをつくるときに、音を協和するようにずらすことができるし、管楽器も音の高低を微調整することが可能なので、現在でも優れた指揮者やオーケストラは、純正律でハーモニーをつくることができる。
純正律とは異なる方法も編み出された。
転調できない欠点を補うために、3度を協和して響くように調律することで、近い調性に転調することを可能にするミーントーンという音律もつくられた。モーツァルトの時代にはよく用いられたといわれている。しかし、これはせいぜいフラットやシャープが３つくらいまでの調性での転調が無理なくできるが、それ以上の臨時記号がつくと、協和しなくなるそうだ。モーツァルトの音楽が、だいたい臨時記号３つまででほとんどが作られているのは、そのためだろう。
バッハの「平均律クラビア曲集」といわれる鍵盤楽器のための音楽は、平均律を想定して書かれたのではないといわれている。24の調性をひとつずつ割り当てた24曲で成立した曲だが、そうした転調が可能なような調律が使われたらしいとされるが、厳密には、どのような調律だったかはわからないとされている。（ヴェルクマイタスーという調律を用いたというのが有力説とされるが、ヴェルマイスターの調律も複数あったようで、正確な方法はわかっていないようだ。）
複雑な音の重なりでの協和性の実現と、自由に調性を変化させることという、主にふたつの要求をともに満たす方法は、完全な形で実現することができないことは、科学的に証明される。したがって、ふたつの目的をできるだけ実現するために、平均律が考案された。
音の高低は、周波数の比できまるわけだが、１２音がすべて均等の比になっているのが平均律である。均等だから、どの音で始めても、その後の音の配列は均等になっているし、したがって、転調は自由にできることになる。その比は、順に２の１２乗根をかけていくという音列である。１２回かければ、２倍になるから、完全なオクターブがえられる。
平均律
平均律は、自由な転調を実現したが、どの音の重なりもオクターブ以外は協和しない。ピタゴラス音律の作り方でわかるが、できるだけ単純な分数で比が表されるふたつの音が、協和する。つまり、音の協和というのは、「有理数」の世界で生じる現象なのだが、２の１２乗根は無理数だから、協和する音程がオクターブだけになってしまう。平均律で調律されたピアノは、ドミソの和音も濁る。
バッハの「よく調律されたクラビアのための曲集」が、日本では、「平均律クラビア曲集」と訳されてきたことも関係しているようだが、バッハの時代から、平均律が普及したと思われがちだが、実際に平均律が主要な音律として使われるようになったのは、１９世紀後半であるという。これは、次回のテーマである鍵盤楽器に関わってくるので、詳細は次回になるが、ピアノが生まれたのはベートーヴェンの時代であり、様々な改良がなされて、いまのピアノのように完成され普及したのが、１９世紀半ばであるとされる。そして、ピアノはあらゆる楽器の王者としての地位を占め、その機能性から、平均律がもっともよく適合していたわけである。
平均律の欠点
音感の鋭い人は、平均律があまり好きではないような気がする。私は、音感がまったくだめなので、平均律を不自然に感じたことはないが、絶対音感をもっていて、しかも、ハーモニーに敏感、そして、調性感覚が鋭い人は、平均律を嫌う。必要悪程度に思っているのかもしれない。私が所属している市民オケで、ドボルザークの新世界交響曲をやっていたとき、出だしのチェロの音程がなかなかあわなくて指揮者が困ってしまい、「みなさん、平均律のピアノでもいいですから、しっかり音をあわせて練習してきてください」と懇願するようにいったことがある。平均律でも仕方ないという言い方だった。
また別の指揮者は、いつも調性感覚を強調する。いまEsdurであるはずなのにち、何調かわからない、などといって、変ホ長調で響くまで、やり直すのである。「それで変ホ長調だ」と満足されても、私には、何が変わったのかは、まるで感じ取れない。こうした指揮者のような人たちには、調性はそれぞれまったく別の響きをもっているらしい。平均律は、そうした完全な調性感覚を相当程度薄めてしまうとされている。
２０世紀最高のピアニストのひとりにポリーニというひとがいる。しかし、強固なポリーニ批判派もいて、熱心にブログなどにその批判を書いているのだが、そのポイントは、ポリーニには調性感覚がないということらしい。ドビッシーの前奏曲集を友人に聞かせて、他のピアニスト（誰かは書いてなかったと記憶する）とポリーニの演奏を比べ、他のピアニストが転調すると、響きが変わり、調性が変わったことがわかるのに、ポリーニの演奏だと、そうした転調の感覚がない、というのである。もし、それほど明瞭に調性感の違いが生じているのだかしたら、おそらく、ピアノの調律の段階で、そのドビッシーのひとつひとつの曲にあわせて、ミーントーンのような転調可能な調律を採用しているのではないだろうか。ポリーニは、平均律で演奏しているとすれば、違いは明瞭にでるのかもしれない。ふたりとも、平均律で調律したピアノを使えば、そのような調性の違いを出すような演奏が可能ではないと思われるのだが。
ポリーニは、シェーベルク以降の現代音楽を得意とするピアニストで、特に１２音音楽のシェーンベルクの名演を残している。１２音音楽は、平均律そのものを前提とした音楽理論に基づいているから、ポリーニ自身が、ピアノ音楽では、調性の変化を重視するという立場ではないのかもしれない。
ピタゴラス音階から平均律にまで至る道筋は、要するに、理論的に矛盾する物理現象を、演奏という実践的なレベルでどのように、カバーしていくか、何を解決し、何を我慢するか、という葛藤の展開なのである。解決不可能な課題だから、いまでもそれぞれの音律は消えることなく、使われており、しかも、音程をつくれる楽器の場合には、平均律を主体にしながらも、他を併用して、ほしい響きを実現している。まさした、多様なもののぶつかり合いによって、発展があるという典型例なのである。
１２音音楽のような、徹底した平均律依拠の音楽は、かえって、広く受け入れられることがないのだとも解釈できる。